To help me explore Kotlin I’ve been writing toy projects. This project is for traversing a graph and finding the minimum distance between two nodes. The algorithm I put together will handle both directed and undirected graphs with weighted edges. My implementation is modeled closely to the Dijkstra’s Shortest Path approach, but should not be considered an example of that algorithm (because I have not checked to be sure my implementation matches the actual algorithm).

The source code for this project can be found here: https://github.com/jeffcardillo/KotlinGraphTraversal

Undirected Graph

Figure A shows the undirected graph my program will build and run tests against. With an undirected graph, you can move both ways across an edge. For example, by adding an edge from A –> B, you can also move from B –> A.

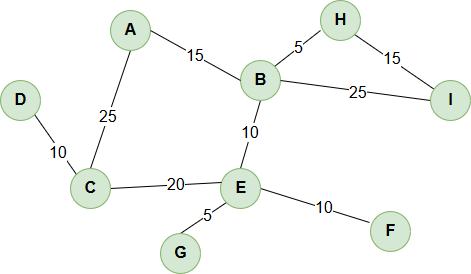
Figure A. (Above)

The output of my program building the above graph and then calculating the minimum distance to and from some nodes:

Building Undirected Graph for Figure A.

A <---> B (15) 
A <---> C (25) 
B <---> E (10) 
B <---> H (5) 
B <---> I (25) 
C <---> D (10) 
C <---> E (20) 
F <---> E (10) 
I <---> H (15) 
E <---> G (5)

Distance A ---> A = 0 
Distance A ---> B = 15
Distance A ---> C = 25
Distance A ---> D = 35
Distance A ---> E = 25
Distance A ---> F = 35
Distance A ---> G = 30
Distance A ---> H = 20
Distance A ---> I = 35
Distance E ---> F = 10
Distance D ---> I = 60
Distance B ---> F = 30
Distance A ---> "No Path" = -1

Directed Graph

Figure B shows the directed graph my program will build and run tests against. With a directed graph, you can only move a single direction across an edge (in the direction the arrow points). For example, by adding an edge from A –> B, you can only move from A to B with that edge. You cannot move from B –> A with that edge.

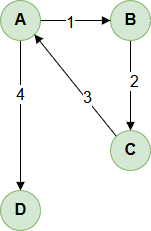
Figure B. (Above)

The output of my program building the above graph and then calculating the minimum distance to and from some nodes:

Building Directed Graph for Figure B.

A ---> B (1)
B ---> C (2)
C ---> A (3)
A ---> D (4)

Distance A ---> B = 1
Distance A ---> C = 3
Distance A ---> D = 4
Distance B ---> D = 9
Distance C ---> A = 3

While I’ve kept my directed and undirected graph examples separate, there is no limitation that requires a graph to be all one type or the other. You can mix directed edge with undirected edges in your graphs.