For the full source code of this project please visit the GitHub repo: https://github.com/jeffcardillo/SpinningCylinderView

I came across some art by Dave Whyte, particularly this piece, and was inspired to write some code! At some point I’d love to build the whole piece in code, but I started thinking about ways to render a 3D looking cylinder on a 2D canvas. The solution I came up with is to manipulate simple shapes based on the periodic changes of sine and cosine functions over time.

I built this sample in Android using Kotlin. I created a custom view called CylinderView that will render a single spinning cylinder. You can add multiple instances of this view to a layout (as shown in the gif below), and even set the colors and spin direction of the cylinders using xml properties.

Note: Currently I have it so that a cylinder that spins in the “up” direction will start at the PI/2 phase (quarter turn).

Progression

When thinking about how to draw a spinning cylinder I imagined two circles oscillating up and down in opposite directions. The first thing that came to mind was to utilize the cosine function because this oscillates between 1 and -1. As a reminder, the sine and cosine functions look like the following:

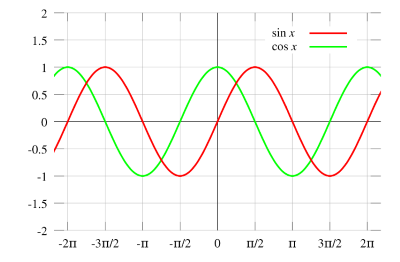
Using just the cosine function I was able to make two circles oscillate opposite each other. At time 0 the cosine function will start at value 1 and decrease to -1 at time = PI, and then increase back to 1 at time = 2 * PI.

Next, I wanted to change the drawing order of the circles so that as they “spun” the top and bottom circle would switch which appeared above the other. Currently I’m just doing this by checking if the cosine value is decreasing or increasing and changing the drawing order appropriately. Note that this gif looks funny out of context because the color jumps from one circle to the other, but this represents the outside vs. the inside of the circle being shown. The next visual will tie this concept together:

Now I needed to show perspective where it would model how a cylinder would look turning away or turning toward you. To do this I wanted to modify the height of the circle. Note that an end of a cylinder would look like a perfect circle when it faced you directly, and then “squish” has it turned away from you. For this I decided to use the sine function. Notice in the graph above that sine moves to 0 as cosine moves to 1. Using this to modify the circle height gives us this:

Now I just need to connect the circles with a body piece. Just a simple rectangle. I will first show the body drawn as a different color so that you can see it distinctly:

And finally, I just made the body the same color as the “bottom” circle:

And now I have a spinning cylinder! It’s just two circles and a rectangle being manipulated with simple math!